変数選択(Feature Selection)の実装と改善の確認

クリックでコードを表示

##import
import pandas as pd
import numpy as np
from IPython.core.display import display
from tqdm import tqdm_notebook as tqdm
from copy import deepcopy as cp

##Visualization
import plotly.offline as offline
import plotly.graph_objs as go
offline.init_notebook_mode()

##visualization
from ipywidgets import interact
#from bokeh import mpl
from bokeh.plotting import figure
from bokeh.io import output_notebook, show, push_notebook
from bokeh.layouts import gridplot
from bokeh.palettes import Category10 as palette
from bokeh.resources import INLINE
output_notebook(resources=INLINE)
import itertools

##import sklearn
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix, roc_curve, roc_auc_score, precision_recall_curve, average_precision_score, auc
from sklearn.feature_selection import SelectKBest, f_classif, RFECV

import boruta_py

## statistical visualization
from string import ascii_letters
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Kozuka Gothic Pro'
%matplotlib inline

はじめに

前回の記事で、変数選択(Feature Selection)についてまとめました。

aotamasaki.hatenablog.com

今回は実際に実装してみます。目的を見失うのを防ぐために、何が目的でどんなことをするのか実験設定を明記します。

実験設定

目的

いくつかの変数選択手法によって変数を選択し、モデルの改善を確かめる。

用いるデータ

irisとかもう見すぎて飽きてるのでKaggleから取ってきました。

Credit Card Fraud Detection | Kaggle

このデータは、クレジットカードのデータから不正使用されたかどうか当てるタスクに用いることができます。ただしオリジナルデータは機密情報で会社としては公開できないので、このデータはオリジナルのデータをPCAしたものになります。説明変数の実態がなんなのかわからないのでハンドクラフトに特徴をピックアップすることができず、今回の変数選択手法を試すのにはぴったりなデータセットだと思います。ただし、Classが1であるサンプルが著しく少ないインバランスなデータです。中身を見てみるとこんな感じです。

##acquire data
df = pd.read_csv('./creditcard.csv')
df.head()

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V21	V22	V23	V24	V25	V26	V27	V28	Amount	Class
0	0.0	-1.359807	-0.072781	2.536347	1.378155	-0.338321	0.462388	0.239599	0.098698	0.363787	...	-0.018307	0.277838	-0.110474	0.066928	0.128539	-0.189115	0.133558	-0.021053	149.62	0
1	0.0	1.191857	0.266151	0.166480	0.448154	0.060018	-0.082361	-0.078803	0.085102	-0.255425	...	-0.225775	-0.638672	0.101288	-0.339846	0.167170	0.125895	-0.008983	0.014724	2.69	0
2	1.0	-1.358354	-1.340163	1.773209	0.379780	-0.503198	1.800499	0.791461	0.247676	-1.514654	...	0.247998	0.771679	0.909412	-0.689281	-0.327642	-0.139097	-0.055353	-0.059752	378.66	0
3	1.0	-0.966272	-0.185226	1.792993	-0.863291	-0.010309	1.247203	0.237609	0.377436	-1.387024	...	-0.108300	0.005274	-0.190321	-1.175575	0.647376	-0.221929	0.062723	0.061458	123.50	0
4	2.0	-1.158233	0.877737	1.548718	0.403034	-0.407193	0.095921	0.592941	-0.270533	0.817739	...	-0.009431	0.798278	-0.137458	0.141267	-0.206010	0.502292	0.219422	0.215153	69.99	0

5 rows × 31 columns

用いる変数選択手法

本記事のメインディッシュです。

• Filter Method
  • 目視
  • sklearn
• Wrapper Method
  • sklearn
  • Boruta

Filter Method2つとWrapper Method2つで、後で述べる評価指標で比較したいと思います。

用いる判別器

ロジスティック回帰を用いて行います。理由としては、計算が軽量であることや線形分離で判別できそうということが挙げられます。(あとで可視化します。)

評価指標

10CVでRP-AUC(PR曲線の下側の面積)の標本平均を用います。PR曲線はROC曲線の親戚のようなもので、インバランスデータを評価するのに適しています。詳しくは過去の記事を見てください。

aotamasaki.hatenablog.com

行わないこと

• インバランスへの対応(用いるデータはClass==1が著しく少ないデータになっています。)
• パラメーターサーチ
• このデータに対してどの判別器が適しているのか
• クラス分類をするための閾値の設定
• この判別に対して最終的なモデルを示す

つまり、変数選択の結果、判定器が改善されたかだけを見ます。

データを少し見てみる

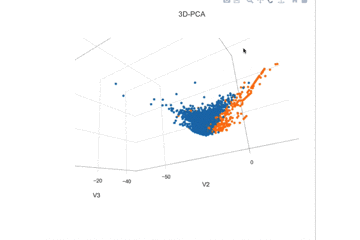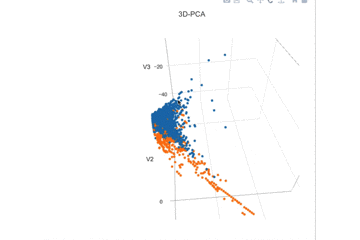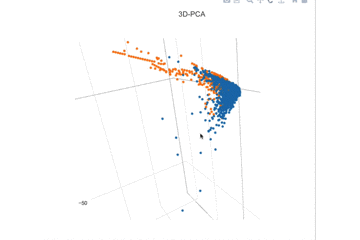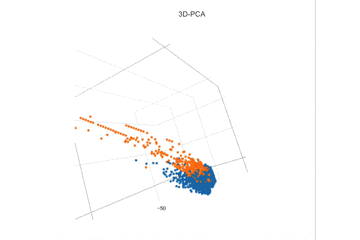
datasetのV1~V3を可視化してみます。これだけでもなんとなく線形分離可能なんじゃないかと予想できます。

クリックでコードを表示

df0 = df[df.Class == 0]
df1 = df[df.Class == 1]
##random under sampling
df0u = df0.sample(frac = 0.04)
## make trace
trace0 = go.Scatter3d(
    x = df0u.V1,
    y = df0u.V2,
    z = df0u.V3,
    name = 'class0',
    mode = 'markers',
    #opacity = 0.4,
    marker = dict(
        size = 3
    )
)
trace1 = go.Scatter3d(
    x = df1.V1,
    y = df1.V2,
    z = df1.V3,
    name = 'class1',
    mode = 'markers',
    marker = dict(
        size = 3
    )
)
## concatnate traces
data = [trace0, trace1]

## define layout
layout = go.Layout(
    title='3D-PCA',
    width=700,
    height=600,
    scene = dict(
        xaxis = dict(
            nticks=4, range = [min(df.V1),max(df.V1)], title='V1'),
        yaxis = dict(
            nticks=4, range = [min(df.V2),max(df.V2)], title='V2'),
        zaxis = dict(
            nticks=4, range = [min(df.V3),max(df.V3)], title='V3')
    ),
    showlegend=True)

fig = dict(data=data, layout=layout)
offline.iplot(fig)

すべての特徴を用いた場合

変数選択が有用ということを示すには、比較対象が必要です。すべての特徴を用いてロジスティック回帰を行った場合に、どれぐらいのスコアが出るのか確認してから変数選択した場合と比較しましょう。

##make matrix
X = df.drop('Class', axis=1)
y = df.Class

def print_pr_auc_score(X, y):
    ##10-foldCV, LogisticRegression, PR_AUC
    pr_auc = cross_val_score(LogisticRegression(), X, y, scoring="average_precision", cv=10)
    print('各分割でのスコア:',pr_auc)
    print('\nその平均:',np.mean(pr_auc))

print_pr_auc_score(X, y)

    各分割でのスコア: [ 0.63098597  0.84872876  0.94781101  0.75652943  0.66064561  0.65631867
      0.91236083  0.66456285  0.82682719  0.72947952]
    
    その平均: 0.76342498463

すべての何も考えず特徴を用いたとき、0.763となりました。これを基準にします。

Filter Method

まずFilter Methodによる変数選択を行ってみます。今回、特徴(説明変数)が連続値で、目的変数がカテゴリーなので、前回の記事の表に従うとLDAを用いて、目的変数に対して特徴が効いてるのか見ることになります。がしかし。sklearnで楽にやりたかったこともあり今回はANOVAのF値を指標にしました。これは、sklearn.feature_selection.SelectKBestでf_classif(判別分析用)を指定したときのスコアになります。 ANOVAのF値については、いろいろ検索してみましたがこちらが私的にわかりやすいと感じました。

分散分析とは何か？（データの変動からいかにして誤差と処理による変動に分けるか？）

(このF値とF分布を用いると検定の枠組みに持っていくことができて、その特徴がどの程度の確率で有意なのかも定量的に判断することができますが今回は考えないことにします。)

さて、では実際に変数選択してみましょう。まずは各クラスごとに各特徴の確率分布を描くことによって、効いてそうな特徴を目視で選択してみることにします。

目視により選択

すべての説明変数の確率分布を表示してみました。図が多いのでここではわかりやすい図だけ示します。

%matplotlib inline
for i in tqdm(range(len(df.columns)-1)):
    g = sns.distplot(df0.iloc[:,i], color='green')
    g = sns.distplot(df1.iloc[:,i], color='red') 
    plt.show()

線形分離でうまく両分布が分かれそうな特徴を選ぶと、V3, V4, V10, V11, V12, V14, V16となりました。これを使ってロジスティック回帰を評価して見ようと思います。

##make matrix
X = df[['V3','V4','V10','V11','V12','V14','V16']]
y = df.Class

##10-foldCV, LogisticRegression, PR_AUC
pr_auc = cross_val_score(LogisticRegression(), X, y, scoring="average_precision", cv=10)
print('各分割でのスコア:',pr_auc)
print('\nその平均:',np.mean(pr_auc))

各分割でのスコア: [ 0.62773678  0.88404438  0.97841888  0.74539661  0.6675292   0.72194876
  0.93095305  0.74931908  0.85213309  0.66366722]

その平均: 0.782114705419

目視で変数選択したときのスコアは0.782となりました。

sklearn.feature_selection.SelectKBestによる選択

目視ではなくもっと機械的に決めます。前述したようにANOVAのF値を用いています。その上位K個を返すといった関数です。 ただし、いくつ変数が選ばれたらモデルとして良いのかわからないため、選ぶ変数の数を探索します。

##make matrix
X = df.drop('Class', axis=1)
y = df.Class

scores=[]
for n in tqdm(range(1,len(X.columns))):
    print('\n説明変数の数n=',n)
    ##select features
    select = SelectKBest(k=n)
    select.fit(X, y)
    mask = select.get_support()
    X_selected = X.iloc[:,mask]
    ##10-foldCV, LogisticRegression, PR_AUC
    pr_auc = cross_val_score(LogisticRegression(), X_selected, y, scoring="average_precision", cv=10)
    scores.append(np.mean(pr_auc))    
    print('平均のPR_AUC:',scores[n-1])

    ## visualization
    plt.matshow(mask.reshape(1, -1), cmap='gray_r')
    plt.tick_params(labelleft = 'off')
    plt.xlabel('使われた特徴. 黒が選択されたもの', fontsize=15)
    plt.show()
    

特徴が選ばれていく様子を示します。

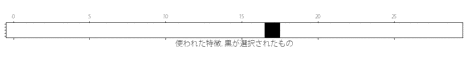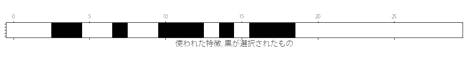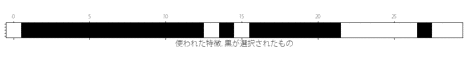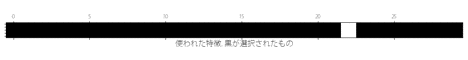
また、用いる説明変数の数とそのときのスコアは以下のようになりました。

説明変数の数n= 1
平均のPR_AUC: 0.650801886077

説明変数の数n= 2
平均のPR_AUC: 0.724352826764

説明変数の数n= 3
平均のPR_AUC: 0.753449924158

説明変数の数n= 4
平均のPR_AUC: 0.776515703337

説明変数の数n= 5
平均のPR_AUC: 0.781896422263

クリックですべて見る

説明変数の数n= 6
平均のPR_AUC: 0.783314413743

説明変数の数n= 7
平均のPR_AUC: 0.783161382675

説明変数の数n= 8
平均のPR_AUC: 0.783224790242

説明変数の数n= 9
平均のPR_AUC: 0.778549498363

説明変数の数n= 10
平均のPR_AUC: 0.777984875316

説明変数の数n= 11
平均のPR_AUC: 0.775272148852

説明変数の数n= 12
平均のPR_AUC: 0.774446873133

説明変数の数n= 13
平均のPR_AUC: 0.767849192086

説明変数の数n= 14
平均のPR_AUC: 0.765752247728

説明変数の数n= 15
平均のPR_AUC: 0.759380398727

説明変数の数n= 16
平均のPR_AUC: 0.761254845928

説明変数の数n= 17
平均のPR_AUC: 0.760012843524

説明変数の数n= 18
平均のPR_AUC: 0.754246272876

説明変数の数n= 19
平均のPR_AUC: 0.744524898983

説明変数の数n= 20
平均のPR_AUC: 0.744022739998

説明変数の数n= 21
平均のPR_AUC: 0.795792325236

説明変数の数n= 22
平均のPR_AUC: 0.799062990337

説明変数の数n= 23
平均のPR_AUC: 0.795809569293

説明変数の数n= 24
平均のPR_AUC: 0.735858783447

説明変数の数n= 25
平均のPR_AUC: 0.764955308213

説明変数の数n= 26
平均のPR_AUC: 0.759512522193

説明変数の数n= 27
平均のPR_AUC: 0.751832822172

説明変数の数n= 28
平均のPR_AUC: 0.73261876595

説明変数の数n= 29
平均のPR_AUC: 0.759085348642

モデルに使う特徴の数とスコアの関係を図示します。

p = figure(
    title = "n vs. PR_AUC", 
    plot_width=500, plot_height=500,
)
p.line(
    range(1,len(scores)+1),
    scores
)
show(p)

21番目の説明変数を加えた途端スコアが大きく伸びました。21番目に追加された説明変数'Time'の確率分布を見てみましょう。

%matplotlib inline
sns.distplot(df0.iloc[:,21], color='green')
sns.distplot(df1.iloc[:,21], color='red')
plt.xlim(-5, 5)
plt.show()

分けられるか微妙ですが、もしかしたら他の変数に対するマルチコが少なく他の変数と組み合わせると有効に働くのかも知れません。上位5つの特徴だけを用いたときと、上位5つ＋'Time'を用いたときを比較しましょう。

##make matrix
X = df.drop('Class', axis=1)
y = df.Class

##select features
select = SelectKBest(k=5)
select.fit(X, y)
mask = select.get_support()
X_selected = pd.concat([df.Time, X.iloc[:,mask]], axis=1)
##10-foldCV, LogisticRegression, PR_AUC
pr_auc = cross_val_score(LogisticRegression(), X_selected, y, scoring="average_precision", cv=10)
print('上位5つのみのとき:',scores[4])
print('上位5つ＋\'Time\'のとき:', np.mean(pr_auc) )

上位5つのみのとき: 0.781896422263
上位5つ＋'Time'のとき: 0.811386618241

Timeも特徴に含めたほうが、結果として一番良いスコアが出ました。SelectKBestでは選ぶことができなかったので、FilterMethodを用いた結果としては、0.782の方を採用します。 Timeは有用な変数だったにもかかわらず、SelectKBestで見逃されたようです。多重共線性を考慮できないのがFilterMethodの問題点です。

Wrapper Method

sklearn.feature_selection.RFECVによる選択

recursive feature eliminationを用いた選択です。

select = RFECV(LogisticRegression(), cv=10, scoring='average_precision')
select.fit(X, y)
mask = select.support_

## visualization
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.tick_params(labelleft = 'off')
plt.xlabel('使われた特徴. 黒が選択されたもの', fontsize=15)
plt.show()

選ばれた特徴でスコアを算出します。

print('選ばれた変数の数',select.n_features_)
print('各変数のランキング',select.ranking_)

選ばれた変数の数 11
各変数のランキング [20 10 11 15  1  5  8 12  1  1  1 16 14  1  1  7  1 17 18  9  2  1  1  1  4
  6 13  1  3 19]

X_selected = X.iloc[:,mask]
##10-foldCV, LogisticRegression, PR_AUC
pr_auc = cross_val_score(LogisticRegression(), X_selected, y, scoring="average_precision", cv=10)
print('平均のPR_AUC:',np.mean(pr_auc))

平均のPR_AUC: 0.788190162305

先程と同じように'Time'が選ばれていません。問題となったTimeも加えて評価してみました。

X_selected = pd.concat([df.Time, X.iloc[:,mask]], axis=1)
##10-foldCV, LogisticRegression, PR_AUC
pr_auc = cross_val_score(LogisticRegression(), X_selected, y, scoring="average_precision", cv=10)
print('\'Time\'を加えたのとき:', np.mean(pr_auc) )

    'Time'を加えたのとき: 0.809050680037

少しだけスコアが上がりました。しかしこれもRFECVが自動的に選んではくれなかったものなので、ここでのスコアは0.788とします。

Borutaによる変数選択

これはrandomForestを用いた変数選択手法の一つで、詳しいアルゴリズムはこちらの3ページに書いてあります。

https://www.google.co.jp/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0ahUKEwiEzMP4p9naAhWBk5QKHbRjC9oQFggoMAA&url=https%3A%2F%2Fwww.jstatsoft.org%2Farticle%2Fview%2Fv036i11%2Fv36i11.pdf&usg=AOvVaw3tyiHN0BCe2fkkAA6xEVDE

##make matrix
X = df.drop('Class', axis=1).values
y = df.Class.values

forest = RandomForestClassifier()
# define Boruta feature selection method
select = boruta_py.BorutaPy(forest, n_estimators=10)
select.fit(X, y)
mask = select.support_

## visualization
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.tick_params(labelleft = 'off')
plt.xlabel('使われた特徴. 黒が選択されたもの', fontsize=15)
plt.show()

X_selected = df.iloc[:,mask]
##10-foldCV, LogisticRegression, PR_AUC
pr_auc = cross_val_score(LogisticRegression(), X_selected, y, scoring="average_precision", cv=10)
print('平均のPR_AUC:',np.mean(pr_auc))

平均のPR_AUC: 0.796296268752

0.796というスコアになりました。適当にパラメーターを決めたり、ロジスティック回帰でいいのかという疑問はありますが、ひとまずこれを採用したいと思います。また、計算時間に関しては、2.5GHzCorei5で4時間程度かかりました。計算中はメモリも2GBぐらい持っていかれたと思います。

実験結果

手法	スコア
なし(全特徴)	0.763
目視	0.782
SelectKBest	0.782
RFECV	0.788
borata	0.796

まとめ

• 4つの変数選択を試してみて、共通してすべての特徴を用いたときよりもスコアが改善した。

• 一番スコアが良かったのはborutaを用いた場合だった。

• borutaは計算時間が著しくかかった。sklearnを用いた場合も結構かかった。用いる判別器によってはborutaと同じぐらいかかるかも知れない。

• 計算量削減の点で、Filter Methodによって判別に寄与しない変数を取り除いてからWrapper Methodを用いるのがよいかもしれない。