特徴量重要度にバイアスが生じる状況ご存知ですか?
なぜこの記事を書いたのか?
決定木をベースにしたアルゴリズムのほとんどに特徴量重要度という指標が存在する。データに対する知識が少ない場合はこの指標を見て特徴量に対する洞察深めることができる。KaggleではEDAのときにとりあえず重要度を見てみるなんてこともするようだ。
しかし、この特徴量重要度にはバイアスが存在していて、特定の条件下では信用出来ないことがある。そういった条件を広く知ってほしいということでこの記事を書いた。
この記事では人工データを生成しバイアスを再現してみた。また、こういったバイアスに対処したという論文を見つけたので軽く紹介する。おまけとしてgainベース以外の特徴量重要度についても紹介する。
目次
- なぜこの記事を書いたのか?
- 想定読者と実験の枠組み
- 特徴量重要度とは?
- 特徴量重要度にバイアスが生じる条件
- 実験
- 特徴量重要度のバイアスに対抗するには?
- 3種の特徴量重要度
- まとめ
- 2020/09/06 追記
- 参考
想定読者と実験の枠組み
想定読者
限定する枠組み
ここでは以下の枠組みに限定して特徴量重要度のバイアスを確認した。
- 2値判別の分類問題
- 決定木をベースにした判別器としてランダムフォレストを採用(仕組みが簡単なため)
- LightGBMといった手法でもバイアスは生じると思いますが誰か検証してくると嬉しい(ついでにどうやって特徴量重要度を算出しているのとかも知りたい)
特徴量重要度とは?
実験的にバイアスを検証する前に特徴量重要度がどうやって算出されているのか復習する。知っている方は飛ばしてもらって構わない。
決定木を用いる機械学習の手法では各特徴量が判別(もしくは回帰)にどれぐたい寄与したかの目安として特徴量重要度を算出できる。 これから先、決定木の学習方法、ランダムフォレストの概要については知っている前提で話を進めるので、不安な方は一回こちらの記事に目を通してほしい
決定木の学習が終わった時点ですべてのノードについて、不純度、どの特徴量で分割したか、を記録している。これらを使って決定木は特徴量重要度を計算している。
scikit-learnの決定木の場合について特徴量重要度の計算方法をもう一度復習しておこう。
…nodeにおけるサンプルの不純度
… nodeで分割したときの改善度
としておこう。
は以下のように計算される。
はnodeにおける総サンプル数に対するそのノードのサンプルの割合である。leftとrightはnodeの子である。図示すると以下のような感じである。

ある分岐について、改善度は以上のように計算できたので、次に木全体で特徴量重要度を得る部分について考える。
決定木ではどの特徴量がどのノードで分割に使用されたかの情報も持っている。ある特徴量Fについて、Fで分割したノードの集合をとする。
このときFの重要度は
と計算される。これはただ単にFで分割したノードの改善度を総和してくださいということだ。
これですべての特徴量について重要度が計算できる。ランダムフォレストにおいては更に決定木の数だけ平均するだけである。
以上が特徴量重要度の計算方法であるが、実はこの時点で重要度のバイアスはすでに生じているのである。
特徴量重要度にバイアスが生じる条件
以下のとき、特徴量重要度は低めに算出される可能性が高い
- その特徴量のデータの解像度(正確にはCardinalityのこと)が低い場合(取りうる数値が荒い)

- 特徴量同士にdependancyがある場合

1. 解像度が低い場合
こんな状況ありえるのか?なんて思われるかもしれないが結構ありえると思う。
測定系の性能の限界などによってこの状況はありえる。例えば、様々な回路の電流と電圧を測って特徴量にしたとしよう。サンプルはある回路で、電流電圧が特徴量である。このとき電圧においては有効数字4桁で計測できたが電流に関しては弱く2桁しか計測できなかった。というような場合は重要度にバイアスが生じる。
2. 特徴量同士にdependancyがある場合
共線性も含めてより一般的にdependancyと書いた。つまり、ある特徴量と同じことを言っている特徴量が混じっていると特徴量重要度にバイアスが生じる。
以下では、特徴量重要度がどの特徴量も同じになるはずの問題設定で1,2の条件を加えてバイアスの存在を確かめる
実験
実験設定
以下の実験では基本的に以下の条件に従う。異なる場合は別途補足する。
- 基本的にデータにかかわらず目的変数はランダムで生成する
- こうすることで、どの特徴量も寄与しないはず(等しく寄与するはず)という状況が作れる
- サンプル数は200、次元数は大体5次元
- ランダムフォレストで使う決定木の本数は100本
- データ生成から学習し終わるまでを1試行として、200試行random_stateを変更し特徴量重要度をバイオリンプロットに示す
たとえば、各次元について標準正規分布から独立にサンプルしたデータに対しての結果を示すと下図のようになる。

見方としては横軸が特徴量を示していて、縦軸が特徴量重要度を示している。
200回試行しているため、バイオリンプロットを用いて分布のように表示している。
当たり前だがこの場合、特徴量重要度にバイアスは存在せず、どの特徴量も同じような重要度をとっていることがわかる。
これから以下について詳細な人工データの設定と結果を見せていく。
- データの解像度が低い場合
- 特徴量同士にdependancyがある場合
- その他の結果
データの解像度が低い場合
データ生成の設定
すべての特徴量は正規分布から独立に生成している。しかし、各特徴量でデータの解像度が違うことを再現するために丸め込みの処理を適応している。
特徴量0がなにも丸め込んでいないもので、特徴量4がめちゃくちゃ丸め込んだ場合である。
具体的には[-3,3]の区間(標準正規分布の3σ)を以下の表に示す数で分割して数字を丸め込んだ。
| 特徴量→ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 分割数→ | ∞(丸めない) | 50 | 20 | 10 | 3 |
結果
ひと目でわかるように丸められている特徴量ほど重要度は下がっている。

データの解像度が荒いことは、決定木がその特徴量で分岐するかどうか検討する回数が少なくなることにつながる。このとき解像度の荒い特徴量の重要度が低く出てしまうのは当たり前だろう。
しかしながら重要度の寄与が等しくなってほしい場面でこうなってしまうのは嬉しくない。
特徴量同士にdependancyがある場合
データ生成の設定
特徴量3と4に単調増加な依存性(dependancy)をもたせた。
具体的には、特徴量0-3まで独立に標準正規分布から生成し、
$$\text{特徴量4}=\exp(\text{特徴量3})$$
となるように特徴量4を作成した。
結果
互いに依存性をもつ3,4は特徴量重要度が減少する結果が出てきた。

聡明な読者の皆様なら決定木がスケーリングに依存しないことをご存知だろう。なので特徴量3と4は決定木からすると全く同じ内容を示すことになる。そのとき、特徴量3で分割しようと特徴量4で分割しようと結果は変わらない。したがって特徴量3,4で重要度を互いに奪い合う結果になってしまう。
その結果3,4の特徴量重要度が減少する。
その他(おまけ)
特徴量の分布でバイアスは生じるか
上記では正規分布ばかりで実験していたが、特徴量ごとに生成する分布を変えたときにバイアスは生じないのか?
結論としては生じない。決定木にとってはある特徴量のサンプルの大小関係のみが大事で、縮尺がどうなっていようが影響はない。そのため、生成する分布の形状を変化させても影響はない。(ただし離散分布ではだめ。データの解像度が異なるからバイアスが生じる。)
各特徴量で生成する分布を変えたときの結果がこちら。バイアスはなさそうだ。

判別に寄与する状況下ではどうなるの?
判別に寄与する特徴量が含まれている場合でも基本的にバイアスの影響が出る。
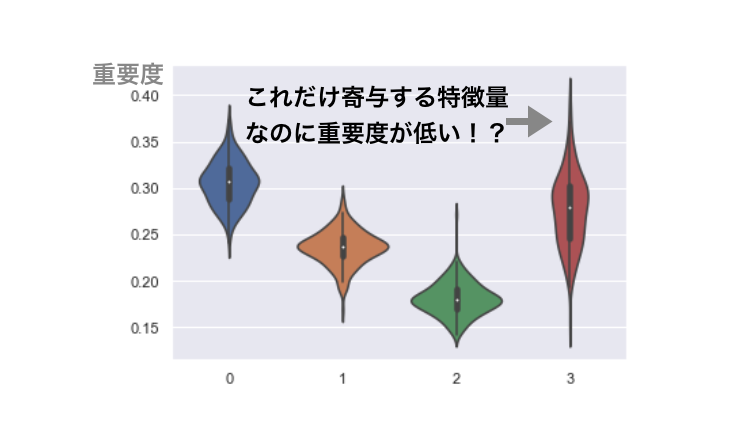
以下に示すのは、データの解像度が一番荒い特徴量のみが判別に寄与する場合の特徴量重要度である。
期待値的には、判別に寄与しない特徴量0よりも低い値になってしまっている。バイアスの影響である。

特徴量重要度のバイアスに対抗するには?
Bias in random forest variable importance measures: Illustrations, sources and a solutionによると以下のようにするとバイアスは防ぐことができるらしい
- cforestを用いる
- R実装しかない?
- 調べるとTJO大先生がブログにしていた
- バギングをしない
- どうやらバギングによるバイアスも存在するらしいがイマイチ理解していない
- 自分の実験でもbaggingをしないでやってみたが、したときとの差がわからなかった。
- 特徴量重要度としてpermutation importanceを用いる
- 特徴量重要度の計算法はいくつかあり、後述する。
- scikit-learnで行われている特徴量重要度はGini importance や Gain importances, mean decrease on impurity importanceと呼ばれるものである
これによりバイアスは防ぐことができるらしいが、この論文では特徴量同士にdependancy(例えば共線性)がある場合については示されていない。おそらくdependancyによるバイアスは残ったままかもしれない。
3種の特徴量重要度
特徴量重要度には以下の3種類存在する。
- split frequency
- gini (gain) importances
- permutation importances
名称については論文やサイトによって揺れがある。
split frequency
単純に分割した回数を重要度とするやり方。判別するのに分岐が多い特徴量が重要でしょうという考え。あまりにも単純なやり方なのであまり使われない印象。
gini importances
scikit-learnでのデフォルト、不純度の改善具合を重要度として採用しましょう、という考え方。詳細は上記(特徴量重要度とは?)で書いた通り。不純度の指標としてgini係数がデフォルトだが、エントロピーが使われることもある。
permutation importances
各特徴量を一つシャッフリング(判別への寄与を無く)したときに、判別精度がどうなるのかみて重要度を決めましょうというアイデアのもの。
アイデアの解説は次のブログが詳しい。
permutation importacesを計算してくれるライブラリ
つかいかたは、このブログにある
まとめ
ここでは、ランダムフォレストの特徴量重要度にバイアスがあることを示した。
バイアスは
- その特徴量のデータの解像度が低い場合(取りうる数値が荒い)
- 各次元が独立ではない場合
に生じる。
対処方法としては
- cforestを用いる
- バギングをしない
- 特徴量重要度としてpermutation importanceを用いる
がある。
しかし、この対処方法でもdependancyを持つ特徴量の重要度のバイアスは取り除けないものと予想している。
dependancyがある特徴量の組がわかっている場合は、セットにして順序を入れ替えることでpermutation importanceの効果を発揮できる。ココらへんの機能はこのブログ に使い方が乗っているので必要になった方は読んでおくと良いだろう。
またcforestのpython実装が見つからなかったのでRがチンプンカンプンな自分にとっては使う障壁が高いのもデメリット。
さいごに、今回はランダムフォレストについてバイアスを確認したが、xgboostやlightgbmではどうかも知りたい。自分はここで力尽きてしまったが余裕のある方に検証してほしい...。 コードはおいておくので必要な方はどうぞ。
blog/bais_of_feature_importances/src at master · masakiaota/blog · GitHub
ちなみにExtremely Randomized Treesでもバイアスは確認できたことを報告しておく。
2020/09/06 追記
Shion HondaさんにLGBMを用いてさらなる調査をしていただけました。4種の特徴量重要度を用いて実験的にその特性を確かめている非常に読み応えがある記事です。
参考
dependancyのバイアスとpermutation importancesについて
permutation importacesを計算してくれるライブラリ
データの解像度とバイアスについて
bmcbioinformatics.biomedcentral.com
ただし、この論文ではデータの解像度ではなく質的変数のuniqueの数で議論が進められている。本質は同じ。ちなみにscikit-learnのRandomForestでは質的変数を直接扱うことができない。target encodingなりで数値に変換する必要がある。 (one-hotはおすすめしない)