中心極限定理による分布収束のアニメーション nを増やすと標本平均はどうばらつくか

モチベーション
中心極限定理は一言で言うと、「平均する対象を増やすと、その標本平均は正規分布に従うようになる」という定理である。これの解釈はあとで与える。 この定理は直感的にはわかりにくく誤用する人も多いため、twitterでhotなトピックになった。本記事はそれに便乗した形で書いた。
本記事では、中心極限定理の直感的解釈を与える。また平均する対象を増やしたときに、標本平均の分布がどのように収束していくのかを可視化する。
以下関連記事
Hello Cyberneticsさんより
ヨビノリさんより
扱う記号の定義
議論を厳密にするために数式及び、確率変数の概念を扱う。確率変数は、まだ実行されていないrand()関数とイメージしてもらうのが良いかもしれない。実現値と言ったときにはrand()を呼び出し、なんらかの乱数をサンプリングした状況を想定していただきたい。
確率変数の従う、確率密度関数(分布) を
と書く。
またこの分布に従う確率変数列を{
}と書く。これらは互いに独立である。
また合計を表す確率変数としてを導入する。
$$ S_n = \sum_{k=1}^{n} X_k$$
このとき、標本平均は以下で計算されることとする。
$$ \frac{S_n }{ n} $$
確率変数Xに対して、期待値や分散はと書くことにする。これは
から計算される値である。具体的な計算方法は確率統計の教科書を参照してほしい。
覚えていて欲しいのは、標本平均はとは異なるという点である。標本平均は実現値から計算しているためばらつく、そのため期待値(真の平均)とは一致しない。
大数の法則
中心極限定理の前にこれを説明しておくと理解しやすい。 これは平均対象(確率変数列)のnが多くなればなるほど、真の平均に近づくという法則である。これは直感的だろう。 理科の実験で、同じ状況でも何回か計測して標本平均するだろう。それは観測値からより真の平均に近い値を引き出したいからである。 式で書くとこんな感じか。
$$ \lim_{n \rightarrow \infty} \frac{\left|S_{n}-E\left(S_{n}\right)\right|}{n} \rightarrow 0 $$
中心極限定理
確率変数を足して割った標本平均も確率変数である。こいつもばらつきがあり、確率変数列から実測値をサンプルするたびに異なる値になる。 では、標本平均の分布はどのような分布に従うのだろうか。この疑問に答えるのが中心極限定理である。
結論から言うと正規分布に従う。証明は難しい(分布の関数が与えられていれば特性関数から計算可能だが一般的な証明は理解していない)ので省略する。
直感的にnを増やすと標本平均の分散はどんどん小さくなるだろう。ここでいい感じに分布を拡大してあげると標準正規分布になる。分散が変わると描画処理が面倒なのでいい感じに拡大することも式に盛り込む。
結果的に以下のようにを定義すると、これは標準正規分布に従う。
$$ T_n = \frac{S_{n}-E\left(S_{n}\right)}{n} \cdot \frac{1}{\sqrt{\frac{V(X)}{n}}} $$
掛け算の先頭は中心化した標本平均である。nを大きくするとこの項の分散が小さくなるが、いい感じに拡大するために、後ろから拡大分をかけている。は定数の認識で構わない。そのときnが大きいと、ルートの部分は小さい値になるため、先頭の項を拡大する。
このようにしたとき、ちょうどnが大きくなるにつれ分散が小さくなる分と拡大しようとする分がつりあって、
の分散は1に保たれる。
ここまで聞いたら、実際にの分布をnを変化させて描いてみようという気持ちになると思うので実際にやってみた。
実験
実験の手続きとしては以下のように行った。
分布としては以下を試した
- 等確率のベルヌーイ分布(コインの裏を-1, 表を+1として表現)
- -1から+1までの一様分布
- λ=1の指数分布
- コーシー分布
以下実験結果である。
ベルヌーイ分布
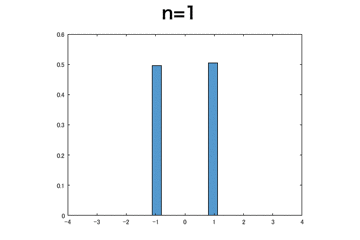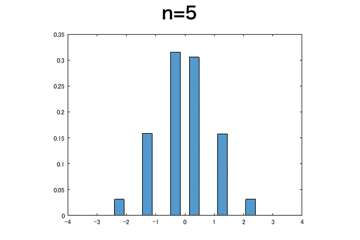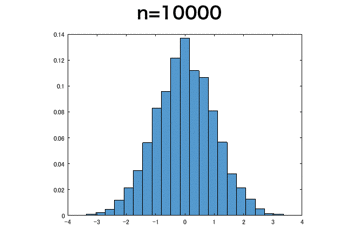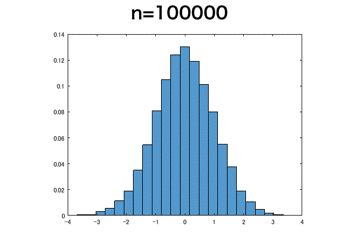
離散分布でもnを大きくするとちゃんと正規分布に収束していっていそう。
一様分布
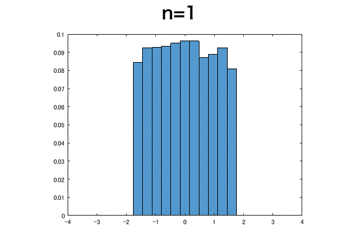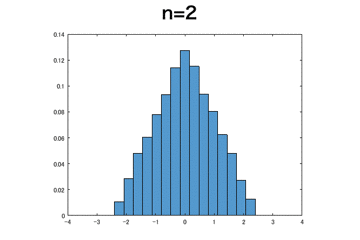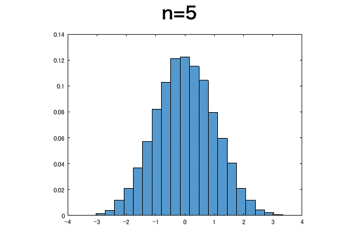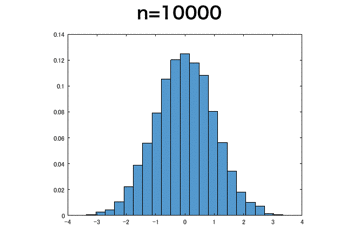
これは上記のベルヌーイ分布と比べるとnが小さめでも標準正規分布に近づいているように見える。
指数分布
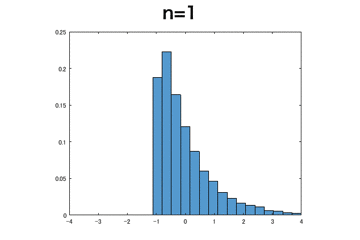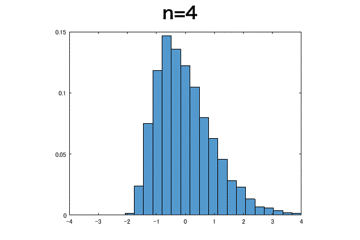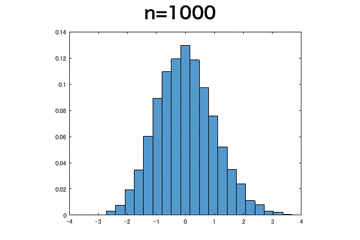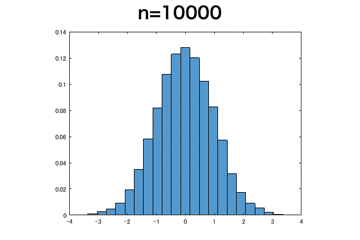
一様分布より収束が遅いが、正規分布に近づいていることが確認できる。
コーシー分布

これは標準正規分布に収束しなかった。コーシー分布は期待値が定まらない分布なので、ある意味期待した通りの結果。どんな分布でも中心極限定理は成り立つという解説が多いが、正確にはコーシー分布以外の分布ならば、が正しい。