学習する天然ニューラルネット

主に機械学習に関する覚書や情報の整理。競プロ水色→Kaggle Master→？

論文読み Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery

深層学習 機械学習

読んだので自分の整理のためにまとめます。

[1703.05921] Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery

導入

扱う問題

  • 医療画像
  • 異常検知
  • GAN (anoGANを提案)

問題意識

  • 画像を入力して病名を判別するのはしんどい
    • 疾患のある画像がすくない
    • 未知の疾患に対応できない

メインアイデア

  • 異常検知問題(正常と異常さえわかればいい)
    • GANを用いる
    • 潜在空間へのマッピングを工夫
    • 異常部位を画像に表示

理論

大筋

GANで正常データの多様体 \mathcal { X } を学習(潜在空間の座標zから画像xを生成可能)
↓
新しい画像\bf{\text{x}} を入力
↓
\bf{\text{x}} を潜在空間 \mathcal {Z}上の座標 \bf{\text{z}_\gamma} に写像(ジェネレーターから見れば逆写像)(ここを工夫)

↓
入力画像と生成画像 G ( \bf{\text{z}_\gamma} ) から異常な部分があれば赤く示す。正常画像を入力すれば生成画像はそっくりなものができるはず。

定式化・アルゴリズム

GAN

$$ \min _ { G } \max _ { D } V ( D ,G ) = \mathbb { E } _ { \mathbf { x } \sim p _ { d a t a } ( \mathbf { x } ) } [ \log D ( \mathbf { x } ) ] + \mathbb { E } _ { \mathbf { z } \sim p _ { z } ( \mathbf { z } ) } [ \log ( 1- D ( G ( \mathbf { z } ) ) ) ] $$ で表されるやつですが、この式を見てもわからないと思います。以下の解説がわかりやすいかと思います。 elix-tech.github.io

新しい画像を潜在空間に写像

ジェネレーターは潜在空間のある座標から画像を生成できます。 $$ G ( \mathbf { z } ) = \mathbf { z } \mapsto \mathbf { x } $$ しかしこの逆写像に対応する関数 \mu ( \mathbf { x } ) = \mathbf { x } \mapsto \mathbf { z }を作るのは困難です。 なのでzを変数として損失関数を作り、勾配法で最適なzを探そうというアイデアです。(この最適なzを \mathbf { z } _ { \gamma }と表記します。)

損失関数は以下のとおりです。λは重み付けだと思いますが、論文中で詳しい解説はありませんでした。 $$ \mathcal { L } \left( \mathbf { z } _ { \gamma } \right) = ( 1- \lambda ) \cdot \mathcal { L } _ { R } \left( \mathbf { z } _ { \gamma } \right) + \lambda \cdot \mathcal { L } _ { D } \left( \mathbf { z } _ { \gamma } \right) $$ \mathcal { L } _ { R } \left( \mathbf { z } _ { \gamma } \right) はResidual Lossで、 \mathcal { L } _ { D } \left( \mathbf { z } _ { \gamma } \right) はDiscrimination Lossです。詳しくは以下で説明します。

Residual Loss

$$ \mathcal { L } _ { R } \left( \mathbf { z } _ { \gamma } \right) = \sum | \mathbf { x } - G \left( \mathbf { z } _ { \gamma } \right) | $$ で定義されます。日本語にすると残差損失でしょうか。各ピクセルの輝度値の差の合計を損失としています。 \mathcal { L } _ { R } \left( \mathbf { z } _ { \gamma } \right) = 0 のとき、入力画像と生成画像は同一です。

Discrimination Loss

$$ \mathcal { L } _ { D } \left( \mathbf { z } _ { \gamma } \right) = \sum | \mathbf { f } ( \mathbf { x } ) - \mathbf { f } \left( G \left( \mathbf { z } _ { \gamma } \right) \right) | $$ で定義されます。これは生成画像 G ( \mathbf { z }_\gamma ) が、正常画像からなる多様体 \mathcal { X } 上にあることを要請するためのものです。ここの \mathbf { f } ( \mathbf {･} )はDiscriminatorの中間表現を用いています。

実験

うまくいかない実験はない論文に載らないので詳細は略します。 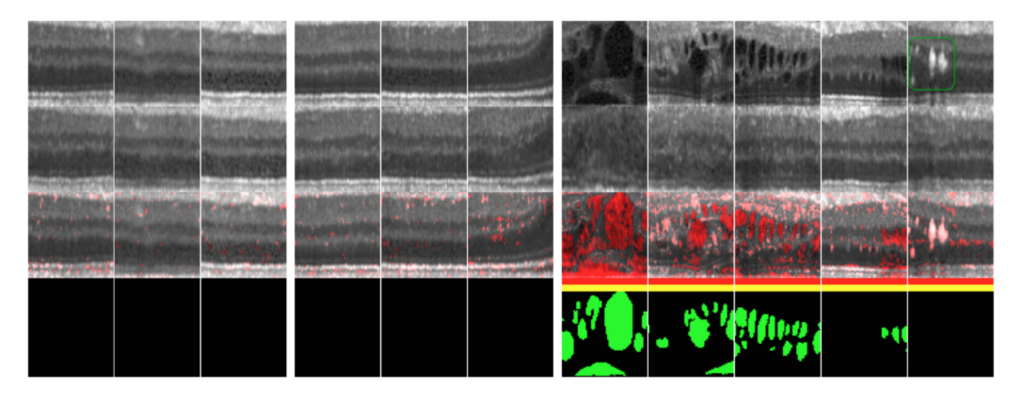f:id:aotamasaki:20180414211624p:plain 一行目が入力画像、二行目がそこから潜在空間にある \mathbf{z}を探してから生成された画像 G ( \mathbf { z }_\gamma ) 、三行目が入力画像と生成画像の残差部分を赤く示した画像

結論

  • GANを使って異常検知ができた。
  • 病変マーカーのマイニングに使えそう
  • Residual Lossのみを用いて画像から潜在空間に写像したほうが良好な結果が得られた。

3つ目に関してあれ？と思ったのですが、流し読みした実験のところでこの事実が判明したのかも知れません。